二叉搜索树（Binary Sort Tree）

左节点<根节点<右节点，增删改查时间复杂度是 logN，但是极端情况下会退化成线性链表（每次插入的节点都是最大的），此时时间复杂度是 N，为了解决这种情况就出现了二叉平衡树

平衡二叉树（AVL）

平衡二叉树可以自平衡，树枝通过左右旋避免退化成线性链表，并且**规定了左子树和右子树的高度差<=1。**但是平衡二叉树过度追求平衡，会频繁左右旋，性能也会有所下降。

增删改查时间复杂度都是 logN

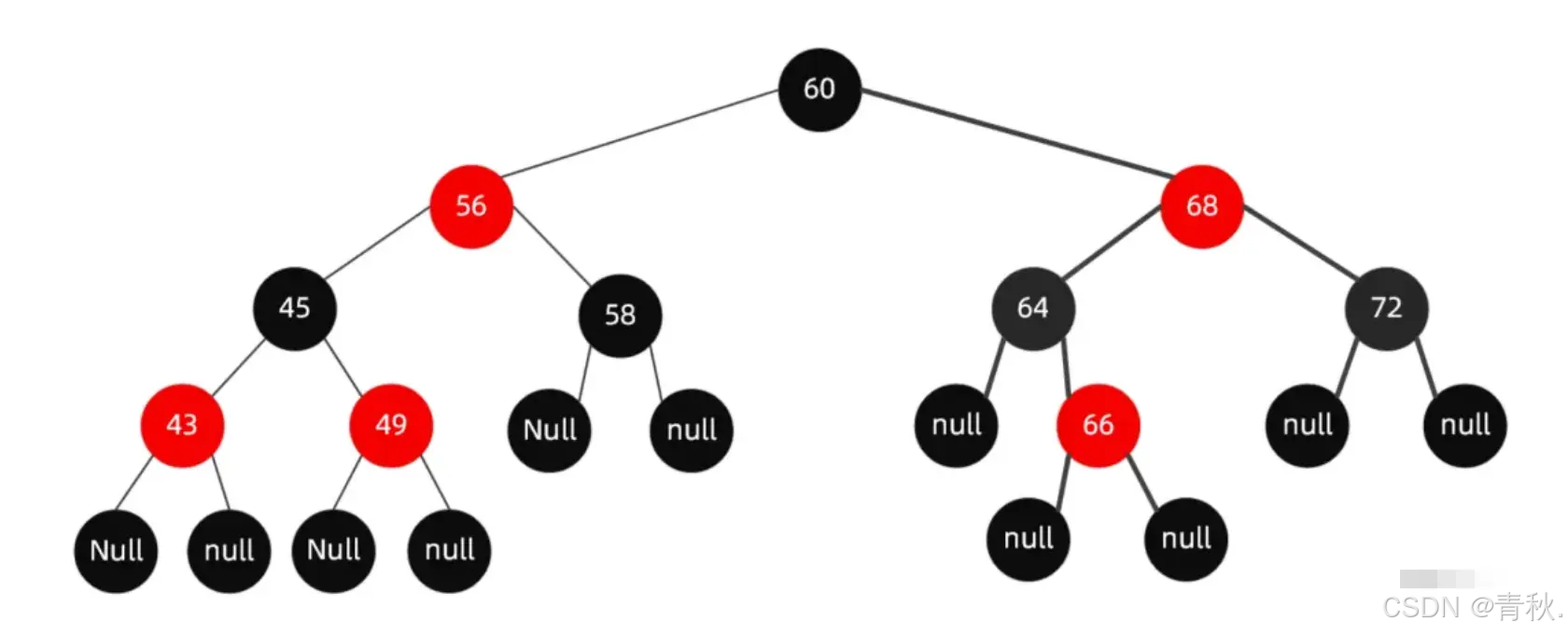
红黑树（Red Black Tree）

自平衡的二叉树，但是和 AVL 不同，红黑树的自平衡是通过左右旋+颜色来实现的，它的节点的颜色为红色和黑色。它不严格控制左、右子树高度差<=1。也是一种解决二叉查找树极端情况下退化成线性链表的数据结构。特点如下：

• 节点非黑即红
• 根节点是黑色，叶子节点都是黑色的空节点。
• 每个红色节点的两个子节点都是黑色。
• 从根节点到叶子节点或空子节点的每条路径上，黑色节点的数量是相同的。

红黑树是保持“黑平衡”的二叉树，即从根节点开始搜索，一直搜索到叶子节点，所经历的黑色节点的个数是一样的。查找效率比 AVL 慢，但是添加和删除则比 AVL 快。

B 树

在存储大量的数据并查询的时候，不论是红黑树还是平衡二叉树都存在深度问题，当其深度过于深，其检索效率会大大降低，所以开发出了 B 树。

B 树的键值存在每个节点中，每个节点的关键字（类似 mysql 索引）出现仅出现一次，

关键字内做一次查找，性能逼近二分查找的，左节点<根<右节点

B+树

在 B 树的基础上，叶子节点之间通过双向指针链接，这就方便了范围查询

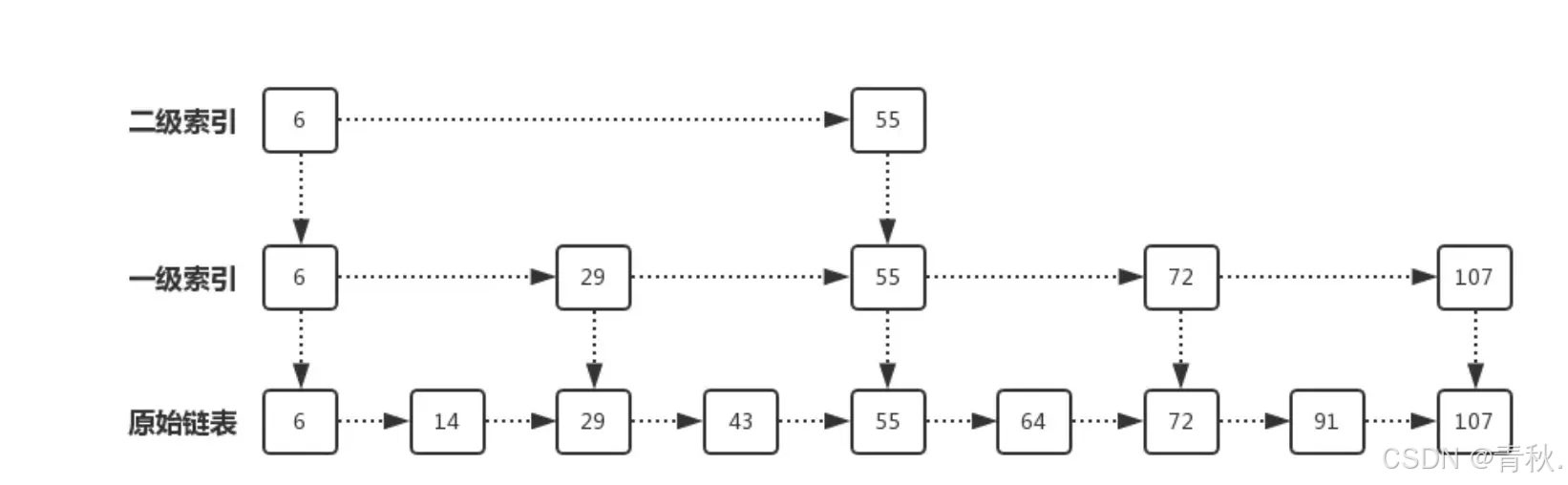
跳表

基于链表的数据结构，通过添加多层索引实现跳跃性查询，特点如下：

跳表中的数据是有序的、跳表中的每个节点都包含一个指向下一层和右侧节点的指针。

redis 就使用跳表实现了 zset